Fuzzy Band Structure of Quantum Dots via Bloch Orbital Expansion: Linking Quantum Chemistry and Quantum Physics Through HPC
- Rafal Tekreeti
- Mar 17
- 3 min read
By: Zeger Hens, Jordi Llusar, and Ivan Infante

Electrons in extended semiconductor crystals behave as waves, free to travel in all directions. The band structure of a semiconductor expresses the unique relation between electron energy and wavenumber – or frequency and wavelength. Semiconductor crystals a few nanometers in size confine electrons in space, thereby turning the electron waves into standing waves. Not unlike sound waves in organ tubes or glass bottles, the wavelength and frequency – or energy and wavenumber – of these standing electron waves depend on the size and shape of the nanocrystals. Larger nanocrystals support longer wavelength and smaller nanocrystals shorter wavelength standing waves; tantamount for lower and higher electron energy. This so-called quantum confinement effect is best illustrated by the changing colors such semiconductor nanocrystals or quantum dots emit when reducing the quantum dot size (see Figure 1). However, just like the wavelength and frequency of a standing sound wave remain related through the speed of sound, the energy and wavelength of standing electron waves still align with the bulk band structure.

Computing the standing wave profiles of single electrons – electron orbitals – in quantum dots is possible through solid state physics approaches. These methods consider semiconductor nanocrystals as bulk crystals but with different boundary conditions that give mathematical expression to the finite crystal size. By construction, these methods yield standing wave profiles in agreement with the bulk band structure. Alternatively, a quantum dot can be approached as a large molecule. Nowadays, quantum chemical packages implemented on high-performance computing clusters, such as the VSC, can calculate molecular orbitals for structures containing several 1000 atoms through the density functional theory. Very often, however, the resulting molecular orbitals show little resemblance to the standing wave profiles deduced from solid-state physics methods. Hence, the question is how to relate both sets of orbitals.
The flexibility of VSC compute starting grant enables researchers to explore new ways of processing quantum-dot orbitals and discover key steps to create next generation materials for display, lighting and infrared sensing.
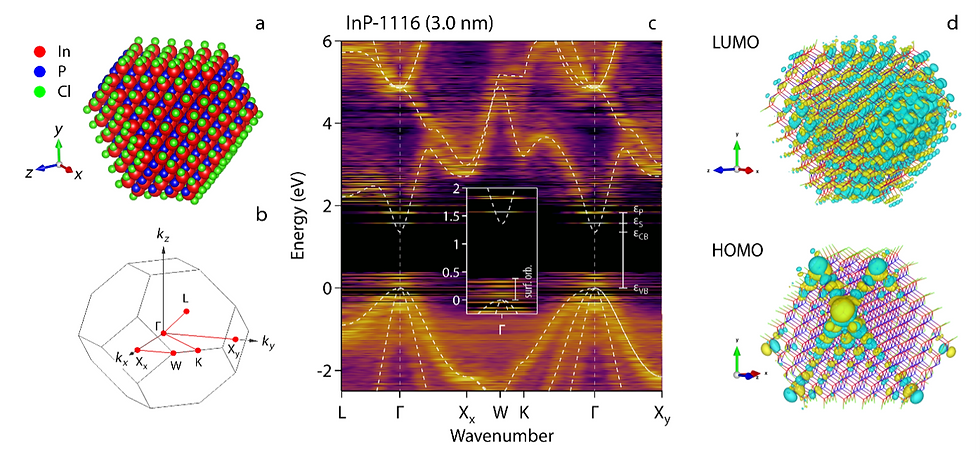
What we introduce is a method – Bloch orbital expansion – for the direct comparison of quantum dot orbitals obtained through quantum chemical methods with the semiconductor band structure. What is computed is a folded Fourier transform of each orbital, which yields a fuzzy quantum dot band structure in an energy versus wavevector diagram. The result is an on-sight classification of quantum dot orbitals. Orbitals whose expansion matches the bulk band structure are standing waves derived from bulk electron waves. Others are quantum-dot specific, typically related to the quantum dot surface. Approaching quantum dots as molecules enabled us to screen orbitals for various quantum-dot geometries with different surface terminations using the VSC. The findings are striking. Seemingly perfect structures directly cut from the bulk crystal yield orbitals dominated by the surface. Only structures with reconstructed or chemically passivated facets yield genuine standing wave orbitals. These are the orbitals needed to get well-defined emission colors from quantum dots. Hence, this unconventional approach to look at quantum dot orbitals will greatly help the development of future quantum dots free of toxic elements such as cadmium or lead for better display and lighting technologies.
Read the full article in ACS Publications here
